第5回 2011年度（前期）数学概評

数学 概評

合格アドバイス

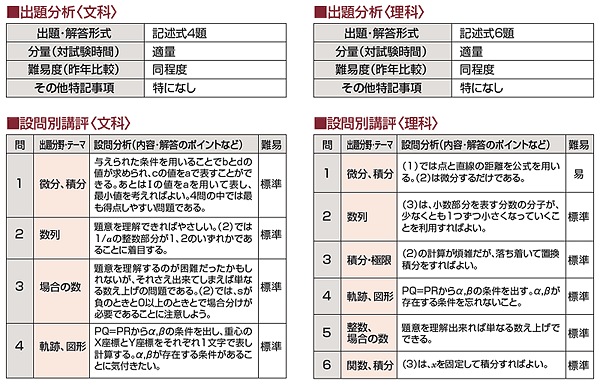
今年度の数学〈理科〉の問題を見て、その概要について述べる。

第1問

第1問。点P(0,1)を中心とする半径1の円を C とする。a を 0<a<1 を満たす実数とし、直線y＝a (x+1) と C との交点をQ、Rとして、（1）△PQRの面積 S (a) を求める。（2）a が 0<a<1 の範囲を動くときに S (a) が最大となる a を求める。

（1）はQRを底辺として、QRの中点をTとするとPTが高さになる。点と直線の距離の公式を使ってもよい。

（2）は微分して増減を調べればよい。この問題は確実に解けるようにしておきたい。最後に答えを載せておくので、まだ解いていない者はチャレンジして欲しい。

第2問

第2問は、数列の問題である。実数 x の小数部分を表す記号＜x＞とそれを含む一般項の式が与えられている。（3）まであって、（1）、（2）は文科と共通。問題文をよく読んで、条件設定を正確に捉えることが大事である。

第3問

第3問は、積分・極限の問題である。点Qが点P(t ,0)を通り原点Oを中心とする円周上をPから出発して反時計回りに道のりL（正定数）だけ進んだ点をQ(u (t )、v (t ))と表す。（1）でu (t )、v (t )を求め、（2）は積分計算を行い、（3）は極限値を求める。少なくとも（1）はできなければならない。

第4問

第4問は、定点Pと放物線上の2点Q、RがQRを底辺とする二等辺三角形をなすときの△PQRの重心Gの軌跡を求める。小問には分かれてはいないが、完答できなくても部分点を得ることはできるので、二等辺三角形になるための条件を求めるなど、できるだけ答案を書くようにしよう。文科と共通。

第5問

第5問は、場合の数の問題である。問題文で与えられた（p 、q ）パターンと呼ばれる整数の並びについて正確に理解できないといけない。思考力が不可欠の問題である。（3）まであって、（1）、（2）の一部は文科と共通。

第6問

第6問は、2次関数と積分の問題である。最後に体積を求めるが、体積計算は東大では頻出である。丁寧に場合分けをして、ミスをしないようにしたい。手間のかかる問題であるので、本番の入試では2次関数の最大値と最小値の差を求める（1）は必ず解いて、（2）、（3）は他の問題を一通り解いてから取りかかった方が無難だろう。

東大の入試問題といえどもすべての問題が難問という訳ではない。入試の標準的な問題を多く演習して、解法と計算力をしっかりと身につけておけば、十分に合格は可能である。できる問題を確実に解いて得点を積み上げることである。理科一・二類志望者は6割、理科三類志望者は7割程度の得点率を目標にしたい。

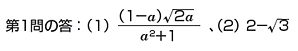
SAPIX YOZEMI GROUP「2011 summer東大合格プロジェクト」より転載

次回は、『2011年度（前期）英語概評』を掲載予定です。